Generalized ODIN

这篇Generalized ODIN被收录在CVPR 2020，是OOD检测的最新的工作。

回顾ODIN

ODIN是OOD检测的一份经典工作了。这个方法以使用softmax值作为分数这个baseline作为基础，并在其上面做了两个改进，增强了softmax分数判别OOD的能力。首先是Temperature Scaling，作者使用如下公式计算softmax值：
$$
S_i(x;T) = \frac{\exp (f_i(x)/T)}{\sum_{j=1}^N \exp (f_i(x)/T)} \tag{1}
$$
第二个改进是Input Preprocessing ，改进的思路来自FGSM，做法是对输入的图片做如下的预处理：
$$
\tilde x = x - \epsilon \text {sign}(-\nabla_x S(x;T)) \tag{2}
$$

作者通过实验证明，上面的两个方法都能够拉大in-distribution和out-of-distribution的样本分数的差距，从而更好地区分开两者。最后，作者设定一个阈值$\delta$，分数低于它就认为是OOD样本，反之则认为是正常样本。

方法简介

作者认为现有的方法如ODIN和马氏距离的方法(以下简称Maha)虽然取得了不错的性能，但是这些方法在设置参数的时候同时使用了in-distribution和out-of-distribution的样本，而现实世界中往往不具备这种条件。基于这种思想，作者以ODIN方法为基础，对ODIN的两个策略做了改进，不再需要OOD样本去调参。改进后的方法具有更高的泛用性，因此称之为”Generalized ODIN”。

The Decomposed Confidence

作者首先解释了softmax分数作为判断依据的局限性。我们使用的softmax分类器的输出$p(y|x)$，实际上并没有考虑输入的domain d，换句话说模型假定$d = d_{in}$。作者用条件概率的形式将其重新表达：
$$
p(y|d_{in}, x) = \frac{p(y, d_{in}|x)}{p(d_{in}|x)}
$$
作者认为这可以解释softmax分类器overconfident的原因，因为$p(d_{in}|x)$按照我们的理解会是一个很小的值，它在分母的位置上就可能产生一个较大的输出。作者认为如果将${p(y, d_{in}|x)}$和${p(d_{in}|x)}$分别建模能够更好地将正常和OOD样本分开，如图所示。

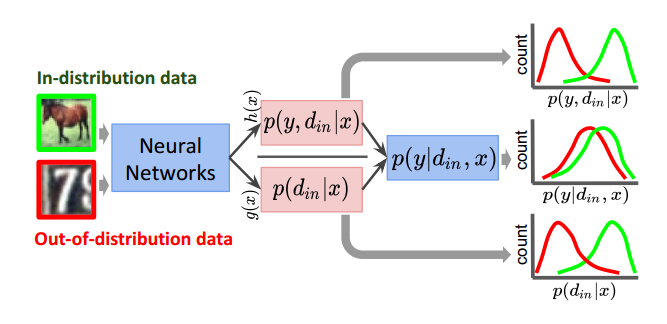
作者定义了一种dividend/divisor结构分类其，定义其输出为
$$
f_i(x) = \frac{h_i(x)}{g(x)}
$$
有了上述的准备，接下来最重要的就是选择合适的$h_i(x)$和$g(x)$了。作者论文中使用的是
$$
g(x) = \sigma(BN(w_g f^p(x)+b_g))
$$
其中$f^p$是网络倒数第二层的输出。关于$h_i(x)$的选择，作者给出了三个不同的版本，

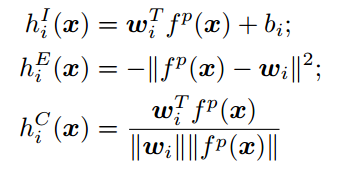
在训练阶段，模型首先根据公式计算出对率$f_i$，接着照常计算softmax和交叉熵损失进行训练。在OOD检测的阶段，作者选择最大的$h_i(x)$或$g(x)$作为分数：
$$
S_{Dconf}(x)=\max_i h_i(x) \ \text{or} \ g_i(x) \tag{3}
$$
作者认为$g(x)$函数可以看作一种可学习的temperature scaling，并且能提供更好的性能。

A Modified Input Preprocessing

ODIN的第二个策略是对输入样本进行预处理，计算方法如公式(2)中所示。本文认为预处理有比较明显的效果，美中不足的是需要在OOD样本上进行调参，如参数$\epsilon$。作者实际上是给出了一种只依赖in-distribution的参数选择方法：
$$
\epsilon^* = \mathop{\arg\max}\limits_\epsilon \sum_{x \in D_{in}} S(\hat x)
$$

实验

在实验部分，作者首先在in-distribution数据集上训练一个分类器，并且在上面调节所有的超参数(例如$\epsilon$)。在测试阶段，作者使用in-distribution和out-of-distribution的样本构建了测试集，根据(3)中描述的方法获得分数，最后计算性能评价指标。

由于本文方法在训练和调参的过程中完全不需要用到OOD的样本，为了公平起见作者修改了ODIN和Maha方法，使他们同样不再需要在OOD数据集上调参。在这种情况下，本方法(DeConf-C)取得了最好的性能：

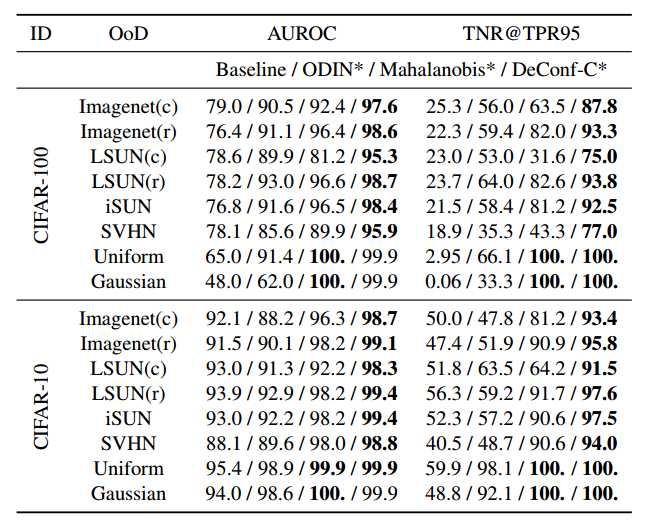
同时，作者也跟原始的ODIN和Maha的性能进行了对比，即使是这种情况下，本文的方法仍然在大多数指标上超过了两者。

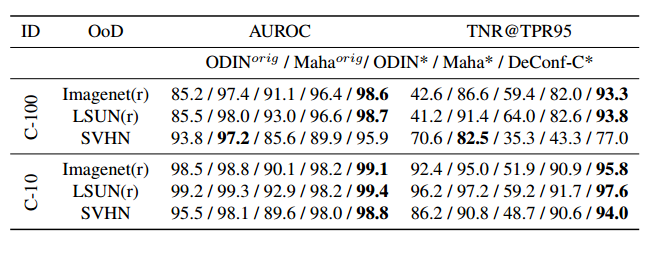
Generalized ODIN在很多指标上确实超过了ODIN和Maha两者，并且不需要在OOD数据集上调参是一个很大的优势。不过它需要重新训练模型，而且得到的模型性能会低于原模型，这是它的主要的劣势。